Today’s Computing Challenges: From physics to applications

Posted on November 23, 2024 by Jan Kaiser

In the months after finishing my PhD, I spent a lot of time thinking about the state of computing and where it’s headed. During this time, I wrote down my thoughts to help organize my view of the computing landscape, and what I ended up with turned out a little longer than I had initially anticipated. Now, I’m sharing it in this blog because I think it would have helped me if I had seen it laid out clearly before I started my PhD journey.

Introduction

In the last decade, there has been significant interest in AI, especially with the recent rise of Generative AI tools like ChatGPT. This surge in interest has led to a new focus on making computing more efficient, with many startups working on specialized AI chips. But even with all the excitement, it’s not always clear to everyone why we’re at this point in computing and what the main challenges are.

Advancing the field of computing today requires tackling the entire computing stack shown in Fig. 1, which spans from fundamental physics principles all the way up to the practical implementation and utilization of computing applications used by customers. The challenge is that many domain experts only know a specific part of this stack. For example, computer architects focus on the fact that Moore’s law is ending but don’t always consider innovations in other areas, while device engineers continue to push Moore’s law forward without thinking much about what’s happening higher up.

To provide a clear overview of where computing stands today and the challenges we face, this blog post will trace the evolution of key technologies in the computing stack. It will start with the foundational principles of Moore’s law and Dennard scaling, explaining their historical impact and eventual limitations. From there, it will explore the rise of multiprocessing and grapic processing units (GPUs) as solutions to these challenges, followed by a discussion on emerging approaches like analog computing and quantum computing.

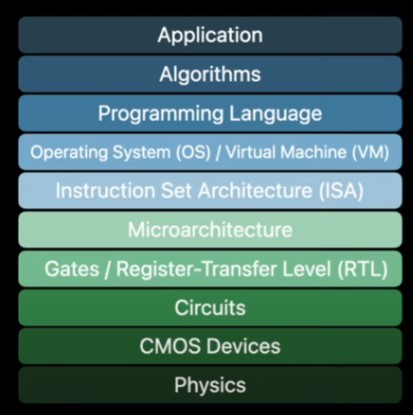
The Era of Moore’s law and Dennard scaling

Prior to the year 2000, the primary driving force behind computing advancements resided at the foundation of the computing stack, rooted in physics. This emphasis on the physical aspects of computing was underscored by the renowned physicist Richard Feynman in his seminal 1959 talk titled “There’s Plenty of Room at the Bottom" (Feynman 1960). Feynman’s central message revolved around the immense potential for miniaturization in computers. His visionary insights laid the groundwork for a future where computers could be dramatically reduced in size.

Building upon this notion, in 1965, Gordon Moore made a significant prediction based on the nascent chip technology of the time. Moore projected that the number of transistors integrated into computer chips would double every two years through a process of shrinking transistor sizes (Moore 1965). This prediction, which later became known as Moore’s Law, not only served as a guideline for the semiconductor industry but also unfolded as a self-fulfilling prophecy. The relentless pursuit of miniaturization propelled computing technology forward, resulting in the present era where we carry pocket-sized devices that outperform room-filling computers from merely half a century ago.

While this technology technology trend is still improving, due to physical limitations where transistors are approaching the size of an atom, Moore’s law has slowed down in recent years. The real problem, however, is the end of Dennard scaling. Dennard scaling is based on a paper by Robert H. Dennard from 1974 (Dennard et al. 1974). Dennard showed that by scaling down transistor sizes and increasing the overall transistor count, the power dissipation per unit area (units: \(\mathrm{W/mm^2}\)) stays constant. While Moore’s law gave us the computing performance, Dennard scaling made sure that the power consumption and thermal management stays sustainable.

Dennard scaling can be understood as follows: The overall power consumption of digital circuit can be described by \[P=\frac{1}{2} \alpha C V_{DD}^2 f + I_{leak} V_{DD}. \label{eq: power}\] Here, \(\alpha\) represents the activity factor, and for sufficiently high supply voltage \(V_{DD}\), the leakage current \(I_{leak}\) can be neglected, making the first term, the dynamic power consumption, dominant. When scaling down transistors by a factor of \(k\), both the capacitance \(C\) and the voltage \(V_{DD}\) decrease by a factor of \(k\). Simultaneously, if we increase the number of transistors per unit area by a factor of \(k^2\) and raise the clock frequency by a factor of \(k\), the overall power per unit area remains constant. This fundamental principle enables enhanced performance with higher transistor density without consuming more total power.

Why did Dennard scaling end?

As mentioned above, for power to reduce with transistor size, the supply voltage has to scale down with the scaling factor \(k\). However, for leakage current to stay negligible, we need to maintain a high ON/OFF ratio for the current that flows through the transistor.

The leakage current in the subthreshold region of a MOSFET is given by \[I_{leak} \propto \exp \Big[ \frac{q (V_{GS}-V_{TH})}{(1+C_{d}/C_{ox}) kT} \Big]\] with gate voltage \(V_{GS}\). The equation shows that to increase the current by a factor of 10 we need around \(\mathrm{60 \ \mathrm{mV}}\) of increased gate voltage as derived below: \[S_{s-th}=\ln(10) \frac{kT}{q} (1+C_{d}/C_{ox}) = 60 \ \mathrm{mV/dec}\] Ideally, we want to have 5-6 orders of magnitude difference between \(I_{ON}\) and \(I_{OFF}\) resulting in a minimum threshold voltage \(V_{TH} \approx 300 \ \mathrm{mV}\). This relation shows that the threshold voltage \(V_{TH}\) for which the transistor will be turned on, cannot be scaled down further while also maintaining an acceptable ON/OFF ratio (Lundstrom 2003). With threshold voltage not going down, the supply voltage scaling cannot be maintained. Indeed, starting with 2005, the supply voltage of modern CPUs was capped at around \(0.9\) V.

Given that \(V_{DD}\) in the power formula cannot be reduced, the clock frequency \(f\) that directly affects the overall performance needs to stay constant as well in order to make sure that the overall power consumption stays the same.

This realization signifies that the conventional approach that had driven performance for over 50 years was no longer effective. The traditional path of relying solely on transistor scaling and increasing clock frequencies reached a point of diminishing returns, necessitating a shift towards alternative strategies to achieve continued advancements in computing performance.

Computer architecture to the rescue?

Since the bottom of the computing stack hit a limit, other approaches for improved computational performance were implemented.

A common way to keep power density constant but still increase performance is by increasing the number of cores per CPU. Since 2005 this has been one strategy to improve performance and also resulted in the emergence of parallel computing machines like GPUs. However, the gain that can be achieved by parallelization is finite and limited by Ahmdahl’s law.

Ahmdahl’s law says that the total speed-up of a process is given by: \[S(s)=\frac{1}{(1-p)+p/s}.\] Here, \(s\) represents the speed-up achieved, and \(p\) denotes the portion of the computation that can benefit from the speed-up. Even if the speed-up \(s\) approaches infinity (such as with an infinite number of parallel cores), there are still resources that do not benefit from the speed-up, indicated by \(1-p\) (for example, the serial portion of a computation). For instance, if \(p\) is 80%, the maximum achievable speed-up is limited to 5x.

Domain-specific accelerators and the Emergence of AI

Around 2015, the impact of Ahmdahl’s law began to impede the performance gains achieved by standard multi-core processors. As highlighted in the Turing lecture delivered by Hennessy and Patterson in 2017, the path to further performance improvements from a hardware perspective lies in specialization and moving away from general-purpose processors (Hennessy and Patterson 2019).

The objective of specialization is to minimize the energy per operation (\(Energy/OP\)), considering that power consumption (\(P\)) can be expressed as:

\[P = \frac{Energy}{OP} \times \frac{OPs}{s}\]

To enhance performance, which is proportional to the ratio of operations per second (\(OPs/s\)), it becomes necessary to reduce the energy per operation (\(Energy/OP\)) since power needs to stay constant.

One of the most computationally demanding domains today is artificial intelligence (AI). Given that AI computations are amenable to specialization, they have received significant attention within the hardware community, encompassing both academia and industry. Numerous strategies have been employed to design specialized processors tailored specifically for AI workloads.

These strategies include a range of approaches. Some well known examples include:

1. Application-specific integrated circuits (ASICs): Custom-designed hardware optimized for specific AI algorithms and tasks, offering high performance and energy efficiency for targeted applications.

2. Graphics Processing Units (GPUs): Originally developed for rendering graphics, GPUs have evolved into powerful parallel processors that excel at AI computations, particularly in tasks involving matrix operations and neural networks.

3. Field-Programmable Gate Arrays (FPGAs): These reconfigurable hardware devices provide flexibility in implementing custom AI algorithms, allowing for efficient acceleration of specific tasks.

4. Tensor Processing Units (TPUs): Google’s specialized AI accelerator designed specifically for machine learning workloads, particularly suited for tasks involving matrix operations and neural networks.

By tailoring hardware designs to the specific requirements of AI workloads, specialized processors offer the potential for significant performance gains and energy efficiency improvements. This focus on specialization represents a shift in the hardware landscape, indicating a growing recognition that addressing the challenges of Dennard scaling and extracting maximum performance requires custom-built solutions aligned with the unique characteristics of target applications.

While many specialization techniques can play a major role, we want to emphasize that the reduction of data movement is a crucial ingredient to efficient computation. Data movement is often the most energy consuming operation in today’s processors (Horowitz 2014). Compute-in-memory (CIM) is a promising approach (Haensch et al. 2023). Here, data movement is reduced by computing directly at or nearby memory cells.

Analog and Mixed-Signal Computing

In addition to optimizing the computer architecture for specific applications, another approach involves harnessing the potential of analog and mixed-signal circuits to enhance performance. This can be seen as another form of specialization.

Analog circuits offer several advantages, including compact continuous representation, fast response times, low power consumption, and improved parallelism. These characteristics make them well-suited for certain computational tasks. However, there are significant challenges associated with analog circuits that need to be addressed.

One of the main challenges is their sensitivity to noise. Analog circuits have lower noise margins compared to digital designs. For instance, if you aim to encode a value between 0 and 1000 as an analog voltage using a supply voltage of 1 V, each value differs by just 1 mV. In contrast, in a digital circuit, the distinction between a 0 and a 1 is typically around 1 V. The increased sensitivity to noise necessitates careful design and noise mitigation strategies to ensure accurate and reliable operation.

Furthermore, analog circuits pose difficulties in programming, design, and testing. The programming of analog circuits is inherently more complex than their digital counterparts due to the continuous nature of signals. Designing and testing analog circuits can also be more challenging, especially when scaling up the circuits to larger and more complex systems because the right tools are not always readily available.

Despite these challenges, ongoing research and development efforts in analog and mixed-signal computing aim to overcome these obstacles and unlock their full potential. Innovations in design methodologies, noise reduction techniques, and advanced testing approaches are being pursued to improve the reliability, scalability, and programmability of analog circuits.

There are also efforts to use noise as a resource and my PhD thesis is about one of these approaches called probabilistic computing. It could be classified as a mixed-signal circuit that specializes on energy-based models and sampling from probability distributions (Kaiser 2022).

Going further up the stack

In the era of Moore’s law, programmers could often rely on continuous improvements in hardware performance without delving deeply into the underlying hardware details. However, with the slowdown of Moore’s law and the increasing importance of specialization, optimizing every layer of the computing stack has become crucial for achieving maximum performance and efficiency.

In the upper layers of the computing stack, there are many opportunities for optimization (Leiserson et al. 2020). Some of these optimizations and their significance are described in the following sections.

System Software and Compilers

System software, including operating systems and device drivers, can greatly impact overall performance. Efficient resource management, scheduling algorithms, and I/O optimizations can significantly improve the utilization of hardware resources and minimize overhead.

Compilers also play a crucial role in optimizing code for specific hardware architectures. By analyzing the code and translating it into optimized machine instructions, compilers can exploit hardware features and generate more efficient executable code. Compiler optimizations, such as loop unrolling, instruction scheduling, and register allocation, can result in substantial performance improvements.

Programming Models and Libraries

Programming models and libraries provide abstractions and tools that allow developers to express their algorithms and tasks in a higher-level manner. These models and libraries provide optimizations and frameworks that are specifically designed for certain domains or hardware architectures, simplifying the development process and improving performance.

For example, frameworks like TensorFlow and PyTorch provide high-level abstractions and optimizations for machine learning tasks, making it easier for developers to utilize specialized hardware accelerators, such as GPUs and TPUs, for faster and more efficient training and inference.

Application-Level Optimization

At the highest level of the stack, application-level optimization involves fine-tuning algorithms, data structures, and code to achieve the desired performance goals. This optimization often requires a deep understanding of the application domain, as well as profiling and benchmarking techniques to identify bottlenecks and areas for improvement.

Additionally, leveraging parallelism, both at the task level and the data level, can lead to significant performance gains. Techniques such as parallel algorithms, distributed computing, and data partitioning can enable efficient utilization of available computing resources and improve scalability.

Quantum Computing

Before we conclude, we want to place Quantum Computing in the landscape we have described. Quantum Computing is in a different category than everything mentioned in this blog post because it is based on a different class of algorithms. The promise of these quantum algorithms is that if quantum computers are scaled up large enough and become capable of running relevant problems, they will do it exponentially better than any classical computer. That means even if quantum computers need to run at cryogenic temperatures and consume much more energy, if they are scaled up large enough, they will outperform anything that is performing computing based on classical physics. While we are still more than 10 years away from reaching such a stage in technology, preparing for a possible breakthrough in Quantum Computing is important for businesses and government entities. Secrets that should stay secret for the foreseeable future and are well enough encrypted today, might not be protected enough for a Quantum Computing age. Encrypted secrets could be stored today and be decrypted by quantum computers later. This is why post-quantum cryptography is an important topic today even if we are years away from realizing a quantum computer of relevant scale.

Conclusion

In conclusion, the evolution of computing technology has reached a pivotal point where further progress requires addressing challenges throughout the entire computing stack. Moore’s law, which fueled decades of performance gains through transistor scaling, has slowed down due to physical limitations and the end of Dennard scaling. This limitation has prompted a shift towards specialization and the exploration of alternative computing approaches.

Specialization in computer architecture, such as increasing the number of cores per CPU and developing domain-specific accelerators, has been instrumental in maintaining performance improvements. Parallel computing machines, like GPUs, have emerged as a result. However, the gains from parallelization are limited by Ahmdahl’s law, which highlights the presence of non-parallelizable components in computing tasks.

Additionally, there is a growing interest in analog and mixed-signal computing as a means to enhance performance. Analog circuits offer advantages such as compact continuous representation, fast response times, low power consumption, and improved parallelism. However, challenges related to noise sensitivity, programming complexity, and scalability must be addressed for widespread adoption.

As we navigate the complexities of the computing landscape, collaboration between experts across the computing stack becomes increasingly important. By addressing challenges at each level, from physics to applications, we can overcome limitations, drive innovation, and shape the future of computing technology. By embracing specialization, exploring alternative computing approaches, and keeping an eye on emerging technologies like quantum computing, we can continue to push the boundaries of what is possible in the world of computing.

References